استخدام معادلة الانحراف المعياري ( الانحراف القياسي) في الحسابات الكيميائية Standard Deviation

استخدام معادلة الانحراف المعياري ( الانحراف القياسي) في الحسابات الكيميائية:

يجب على كل مجموعة من النتائج التحليلية أن يصاحبها مؤشر على مدى دقة التحليل، و هناك عدة طرق مختلفة يمكن للدلالة بها على الدقة يمكن القبول بها. فالانحراف المعياري σ لمجموعة لانهائية من البيانات التجريبية يمكن حسابه نظريا من خلال العلاقة الآتية:

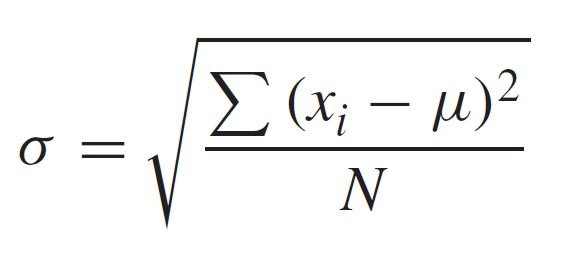
حيث يمثل الرمز x_i القياسات الفردية (في بعض المراجع الاخرى يستخدم الرمز x ) و الرمز μ متوسط لعدد لا حصر له من القياسات (والتي يجب أن تمثل القيمة «الحقيقية»)و العلاقة السابقة تنطبق فقط عندما يكون عدد القياسات التجريبية لا نهائي، أي: ∞→N ، حيث N هو عدد القياسات (في بعض المراجع الاخرى يستخدم الرمز n ). و لكن من الناحية العملية ، يجب أن نحسب الانحرافات الفردية من متوسط عدد محدود من القياسات ، أي القيمة الوسطية لتلك القياسات و التي يرمز لها بالرمز ̅x ، بحيث يفترض أن تكون x̅ → μ لطالما ∞ → N ، على الرغم من أننا لا نملك تأكيدًا على ذلك ،و يمكن حساب ̅x بواسطة العلاقة (x_i /N) ∑ ( أي بجمع جميع قيم القياسات و تقسيمها على عدد القياسات).
و بالنسبة لمجموعة N من القياسات، فإن هناك انحرافات لـ N (متغيرة بشكل مستقل) عن رقم مرجعي معين، و إذا كان الرقم المرجعي هو المتوسط المقدر ̅x ،فإن مجموع الانحرافات الفردية (مع الاحتفاظ بالإشارات موجبة أو سالبة) يجب أن تضاف لحد الصفر ، وبالتالي فإن قيم الانحرافات N − 1 ( أي: N ناقص 1) كافية لتحديد قيمة N. وهذا يعني أنه لا يوجد سوى انحرافات N−1 مستقلة عن المتوسط عندما يتم تحديد قيم N − 1 ، حيث يتم تحديد القيمة الأخيرة مسبقًا. وهنا في الحقيقة استخدمنا ، في الواقع ، درجة واحدة من حرية البيانات في حساب المتوسط ، تاركين N−1 درجة من الحرية لحساب الدقة.
ونتيجة لذلك ، فإن الانحراف المعياري المقدر لمجموعة محدودة من البيانات التجريبية (بشكل عام N أصغر من 30) يماثل تقريبًا σ إذا تم استبدال N−1 ، أي: عدد درجات الحرية ، بقيمة N (ضبط N − 1 للفرق بين ̅x و μ).

و الآن لنفترض أن لدينا القراءات أو القياسات الآتية: 1 ، 2 ، 3 ، 4 ، 5 ،  ، فإن متوسط القراءات ̅x يساوي 3 ، و الإنحراف المعياري S يساوي 1.58 .

مثال لحساب معادلة الانحراف المعياري :

احسب المتوسط و الانحراف المعياري للقراءات التحليلية الآتية: 15.67 و 15.69 و 16.03 .

الحل:

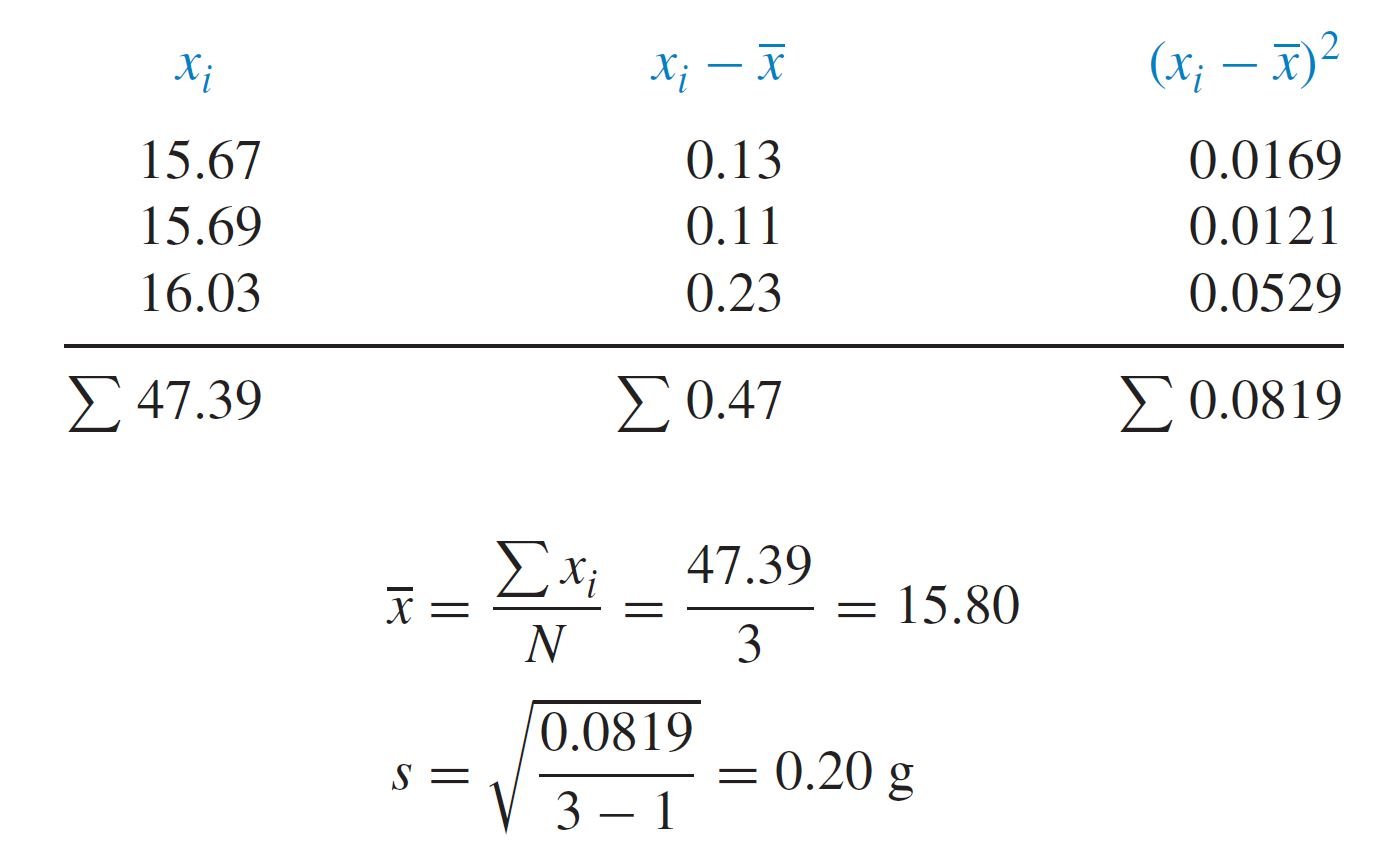
و يمكن استخدام الآلة الحاسبة لحساب الانحراف المعياري للمثال السابق باتباع الخطوات الآتية و التي قد تختلف الشيء البسيط من حاسبة لأخرى:

1 – في العادة تكون شاشة الآلة الحاسبة بالشكل الآتي و لاحظ وجود حرف D على الشاشة للدلالة على أنها بوضعية (mode) الحسابات العادية:

2 – نغير من وضعية الآلة الحاسبة لحسابات الانحراف المعياري بالضغط على زر MODE فتظهر الشاشة الآتية:

3 – ثم نختار STAT بالضغط على رقم 3 ، تظهر الشاشة الآتية:

4 – و من ثم نختار 1-VAR بالضغط على الرقم 1 فتظهر الشاشة الآتية

5 – نقوم بكتابة القراءات بحيث عند إدخال كل قراءة نضغط بعدها زر (=): أي: 15.67 (=) 15.69 (=) 16.03 (=)

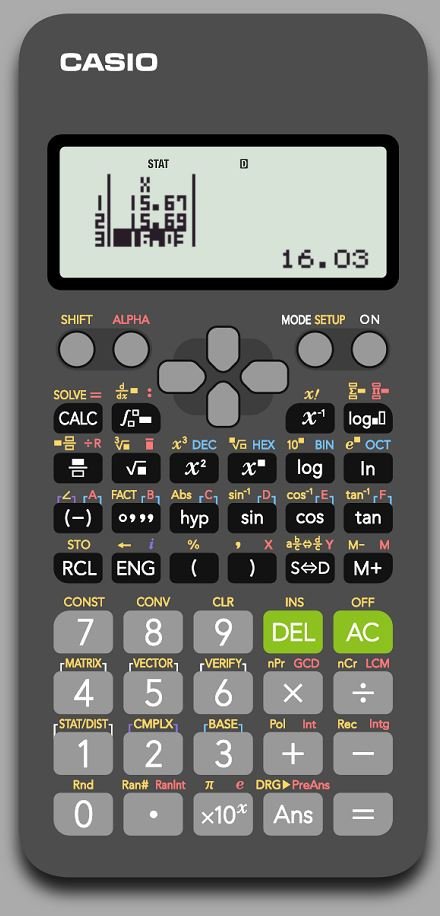
6 – ثم نضغط على الزر AC و من ثم نضغط على الزر SHIFT ثم رقم 1 فتظهر الشاشة الآتية:

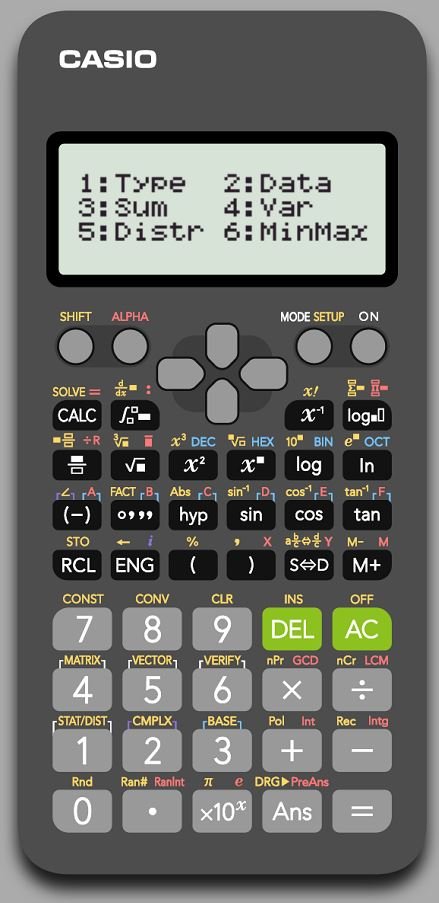
7 – نختار Var بالضغط على رقم 4 فتظهر الشاشة الآتية:

8 – من هذه الشاشة يمكن اختيار الإجابة التي تريدها ، فلحساب الانحراف المعياري للمثال السابق مثلا، نختار sx بالضغط على الرقم 4 ، فتظهر الشاشة الآتية:

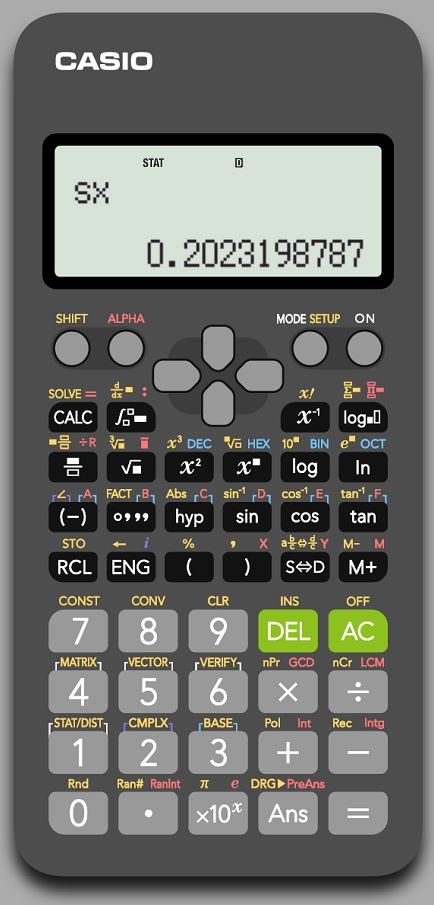
9 – و أخيرا نظغط على زر (=) فتظهر النتيجة كما هو مبين أدناه:

 

بوسترات (لوحات) كيميائية بدقة عالية (أكثر من 25 لوحة) من تصميم الأستاذ أكرم أمير العلي

 

تطبيقات كيميائية من تصميم الأستاذ أكرم امير العلي متوفر للجوالات التي تعمل بنظام أندرويد android على سوق جوجل بلاي google play

1 – تطبيق ملصقات الجدول الدوري باللغة العربية : بطاقات تحتوي على معلومات شاملة و مختصرو في نفس الوقت كل عنصر على حدة (اللغة العربية).

https://play.google.com/store/apps/details?id=com.akramir2

 

2 – تطبيق ملصقات كيميائية: ملصقات بتصميم جميل جدا للكواشف و الأدلة و الزجاجيات المستخدمة في المختبر و كذلك ملصقات و بطاقات لخزانات حفظ المواد و الأدوات الزجاجية .

https://play.google.com/store/apps/details?id=com.akramir

 

3 – إذا كنت تواجه صعوبة في تحضير المحاليل الكيميائية الأكثر شيوعا في مختبرات الكيمياء و الاحياء، فهذا التطبيق سوف يساعدك كثيرا في تحضير المحاليل :

مقالات قد تفيدك :